Sammansatt definition
Sammanställning är metoden för beräkning av räntesats som faktiskt är ränta på ränta där ränta beräknas på investering / initial kapital plus intjänad ränta och andra återinvesteringar, med andra ord ackumulerad ränta ackumuleras till huvudbeloppet beroende på tidsperioden för insättning eller lån det kan vara månadsvis, kvartalsvis eller årligen
Låt oss försöka förstå vad som är sammansatt och hur det fungerar genom några grundläggande exempel
Topp 4 exempel på föreningens kraft
Exempel 1
Shane och Mark beslutade båda att investera 1 000 000 $, men Shane bestämde sig för att investera i enkel ränta, medan Mark investerade i sammansatt ränta i tio år till 10% ränta. Låt oss se vad som händer efter tio år.
Lösning:
Så beräkningen av Shane-investering kommer att vara -

Totalt intäktsbelopp = $ 200.000
Med ett enkelt intresse får Shane $ 2 000 000 efter tio år.
Beräkningen av varumärkesinvestering kommer att vara -

Totalt intjäningsbelopp = $ 259 374
Med sammansatt ränta kommer Marks investeringsvärden att växa till $ 259 374.
Nu bestämde Shane sig för att investera genom sammansättningsmetoder som Mark, och de investerade båda 2 00 000 $ i en takt av 15%.
Beräkningen av Shane-investering kommer att vara -

Totalt intjäningsbelopp = $ 8,09,111.55
Shane förblir investerad i tio år och får det slutliga beloppet till $ 809111,55 med en hastighet på 15%.
Beräkningen av varumärkesinvestering kommer att vara -

Totalt intäktsbelopp = $ 65,83,790.52
Mark är dock tålamod för långsiktiga investerare och förblir investerad i 25 år, och hans investeringsvärde växer till $ 65,83,790.52
Ovanstående exempel visar kraften av sammansättning. Ju längre investeringshorisont, desto större är den exponentiella tillväxten.
Exempel # 2 (Veckovis)
Simon har 7500 dollar i besparingar, och för sin sons collegefond, som kommer att gå på college efter 15 år, bestämde han sig för att investera i amerikanska sparobligationer. Simons mål är att spara 20 000 dollar och den årliga procentsatsen för en amerikansk sparande obligation är 6%. Vad är det framtida värdet av Simon Money efter 15 år?
Lösning:
Given,
- Rektor = $ 7500
- Rate = 6% eller 0,06
- Tidsperiod = 15 år.
- Hur många gånger är det sammansatt på ett år n = 52 veckor
- Framtida värde =?
Så beräkningen av framtida värde kommer att vara -

Formeln för veckoblandning är som nedan.
F = P (1 + r / n) n * t- F = $ 7500 (1 + 0,06 / 52) 52 * 15
- F = $ 7500 (1 + 0,001153846) 780
- F = 18 437,45 $
Så från ovanstående beräkning är det uppenbart att Simons mål att spara $ 20,00 inte kommer att uppnås med ovanstående metoder, men det är närmare det.
Kontinuerlig sammansättningsmetod
Låt oss nu prova ovanstående exempel med kontinuerlig sammansatt formel.
Så beräkningen av framtida värde kommer att vara -

- F = $ 7500e 0,06 * 15
- F = $ 7500e 0,9
- Framtidsvärde (F) = $ 18,447.02
Nu, även med kontinuerlig sammansättning, uppnås inte Simons mål att spara 20 000 dollar för sin sons college.
Låt oss se med månatlig sammansatt formel att hur mycket pengar behövde Simon investera för att uppnå sitt mål att spara 20 000 dollar på 15 år med en APR på 6%?
Så beräkningen av framtida värde kommer att vara -
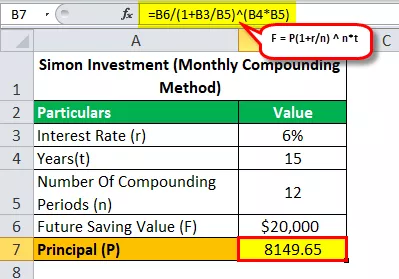
- 20 000 $ = P (1 + 0,06 / 12) 12 * 15
- P = 20 000 $ / (1 + 0,06 / 12) 12 * 15
- Rektor (P) = 8149,65
Så genom att lösa ovanstående ekvation får vi ett svar på 8 149,65 dollar (belopp som Simon behöver investera för att uppnå sitt mål att spara 20 000 dollar på 15 år).
Exempel nr 3 (Effektiv årlig avkastning)
Låt oss säga XYZ begränsad bank ger 10% per år till äldre medborgare för fast insättning, och vi antar här att bankränta kvartalsvis är sammansatt som alla andra banker. Beräkna den effektiva årsavkastningen för 5, 7 och 10 år.
Lösning:
Årlig avkastning i 5 år:
- t = 5 år
- n = 4 (kvartalsvis sammansatt)
- I = 10% per år
Så A = (1 + 10% / 100/4) (5 * 4)
- A = (1 + 0,025) 20
- A = 1,6386
- I = 0,6386 på 5 år
Effektivt intresse = 0,6386 / 5
Effektiv I = 12,772% per år
Årlig avkastning i 7 år:
- t = 7 år
- n = 4 (kvartalsvis sammansatt)
- I = 10% per år
Så A = (1 + 10% / 100/4) (7 * 4)
- A = (1 + 0,025) 28
- A = 1,9965
- Jag = 1,9965 på 7 år
- Effektiv I = 0,9965 / 7
Effektiv I = 14,236% per år
Årlig avkastning i tio år:
- t = 10 år
- n = 4 (kvartalsvis sammansatt)
- I = 10% per år
Så A = (1 + 10% / 100/4) (10 * 4)
- A = (1 + 0,025) 40
- A = 2 685
- Jag = 1,685 på 10 år
- Effektiv I = 1,685/10
Effektiv I = 16,85% per år
Exempel # 4 - (Livräntor: framtida värde)
1 000 dollar investeras var tredje månad till 4,8% per år sammansatt kvartalsvis. Hur mycket kommer livränta att vara värd på tio år?
Lösning:
Så när vi säger hur mycket livränta kommer att vara värd om tio år betyder det här att vi måste hitta framtida värde, och detta viktigt för närhelst det finns ett exempel på livräntor måste vi se vad vi måste ta reda på.
Så, formeln för framtida värde är
FV för livränta = P ((1+ r) n - 1 / r)- P = periodisk betalning
- r = Rate per period
- n = Antal perioder
Så formeln för framtida värde är
- Så här P = $ 1000
- r = 4,8% per år eller 0,048
- r (kvartalsvis) = 0,048 / 4
- r (kvartalsvis) = 0,012
- n = 10 år
- n (Antal gånger blandningen kommer att gälla) = 10 × 4 = 40
Så beräkningen av FV av livränta kommer att vara -

Så nu är FV = $ 1000 (1 + 0,012) 40 -1 / 0,012)
Så genom att lösa ovanstående ekvation får du en FV på $ 50 955,30
Så hur mycket blir livräntan om tio år och svaret är $ 50 955,30
Som ett tillägg kan vi också ta reda på från ovanstående exempel att hur mycket intresse tjänas på tio år.
Som 40 gånger investeras $ 1000, det vill säga en total investering (40 × $ 1000 = $ 40.000).
Så intresse = framtida värde - totala investeringar
- Ränta = $ 50 955,30 - $ 40 000
- Ränta = 10 955,30 $
Så här är det viktigt att förstå att investerare kan tjäna mycket intresse i livräntor. I ovanstående speciella exempel ger en insättning på 40 000 USD i gengäld en total ränta på 10 955,30 USD.
Obs! Du kan ladda ner den ovan angivna Excel-mallen för detaljerad beräkning.








