Vad är korrelationskoefficienten?
Korrelationskoefficient används för att bestämma hur starkt förhållandet är mellan två variabler och dess värden kan sträcka sig från -1,0 till 1,0, där -1,0 representerar negativ korrelation och +1,0 representerar positivt förhållande. Den tar hänsyn till de relativa rörelserna i variablerna och definierar sedan om det finns något samband mellan dem.
Formel för korrelationskoefficient
r = n (∑xy) - ∑x ∑y / √ (n * (∑x 2 - (∑x) 2 )) * (n * (∑y 2 - (∑y) 2 ))
Var
- r = korrelationskoefficient
- n = antal observationer
- x = 1: a variabel i sammanhanget
- y = andra variabeln
Förklaring
Om det finns någon korrelation eller säg förhållandet mellan två variabler, ska det indikera om en av variablerna förändras i värde, då kommer den andra variabeln också att förändras i värde, säg specifikt som kan vara antingen i samma eller i motsatt riktning. Täljardelen av ekvationen genomför ett test och relativ styrka för variablerna som rör sig tillsammans, och nämnarens del av ekvationen skalar täljaren genom att multiplicera skillnaderna mellan variablerna från kvadratiska variabler.
Exempel
Exempel 1
Tänk på följande två variabler, x och y, du måste beräkna korrelationskoefficienten.
Nedan ges uppgifter för beräkningen.

Lösning:
Med hjälp av ovanstående ekvation kan vi beräkna följande

Vi har alla värden i tabellen ovan med n = 4.
Låt oss nu ange värdena för beräkning av korrelationskoefficienten.

Därför är beräkningen som följer,

r = (4 * 25,032,24) - (262,55 * 317,31) / √ ((4 * 20,855,74) - (262,55) 2 ) * ((4 * 30,058,55) - (317,31) 2 )
r = 16,820,21 / 16,831,57
Koefficienten blir -

Koefficient = 0,99932640
Exempel 2
Land X är ett växande ekonomiland och det vill göra en oberoende analys av de beslut som fattas av centralbanken angående ränteförändringar, oavsett om de har påverkat inflationen och har centralbanken möjlighet att kontrollera detsamma.
Nedan följer sammanfattningen av räntesatsen och den inflation som rådde i landet i genomsnitt under dessa år.
Nedan ges uppgifter för beräkningen.

Landets president har kontaktat dig för att göra en analys och ge en presentation om samma i nästa möte. Använd korrelation och avgör om centralbanken har uppfyllt sitt mål eller inte.
Lösning:
Med hjälp av formeln som diskuterats ovan kan vi beräkna korrelationskoefficienten. Behandla ränta som en variabel, säg x, och behandla inflationen som en annan variabel som y.

Vi har alla värden i tabellen ovan med n = 6.
Låt oss nu ange värdena för beräkning av korrelationskoefficienten.


r = (6 * 170,91) - (46,35 * 22,24) / √ ((6 * 361,19) - (46,35) 2 ) * ((6 * 82,74) - (22,24) 2 )
r = -5,36 / 5,88
Korrelationen blir -

Korrelation = -0,92
Analys: Det verkar som om korrelationen mellan räntan och inflationen är negativ, vilket verkar vara det korrekta förhållandet. När räntan stiger minskar inflationen, vilket innebär att de tenderar att röra sig i motsatt riktning från varandra, och det framgår av ovanstående resultat att centralbanken lyckades genomföra beslutet om räntepolitiken.
Exempel # 3
ABC-laboratorium bedriver forskning om längd och ålder och ville veta om det finns något samband mellan dem. De har samlat ett urval på 1000 personer för var och en av kategorierna och kommit fram till en genomsnittlig höjd i den gruppen.
Nedan ges data för beräkning av korrelationskoefficienten.

Du måste beräkna korrelationskoefficienten och komma fram till slutsatsen att om någon relation finns.
Lösning:
Att behandla ålder som en variabel, säg x och behandla höjd (i cms) som en annan variabel som y.

Vi har alla värden i tabellen ovan med n = 6.
Låt oss nu ange värdena för beräkning av korrelationskoefficienten.

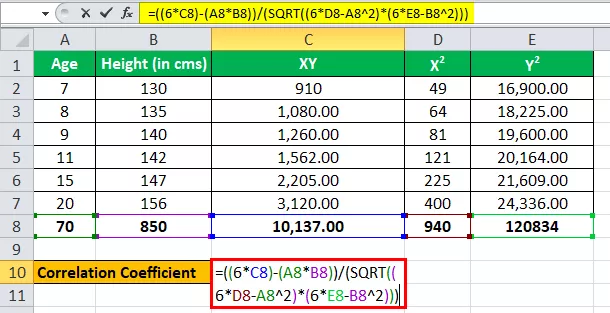
r = (6 * 10,137) - (70 * 850) / √ ((6 * 940 - (70) 2 ) * ((6 * 1,20,834) - (850) 2 )
r = 1 322,00 / 1 361,23
Korrelationen blir -

Korrelation = 0,971177099
Relevans och användning
Den används i statistik främst för att analysera styrkan i sambandet mellan variablerna som övervägs och vidare mäter det också om det finns någon linjär relation mellan de givna datamängderna och hur väl de kan relateras. En av de vanliga måtten som används i korrelation är Pearson Correlation Coefficient.
Om en variabel förändras i värde och tillsammans med den andra variabeln ändras i värde, är det viktigt att förstå det förhållandet eftersom man kan använda värdet på den tidigare variabeln för att förutsäga förändringen i värdet på den senare variabeln. En korrelation har många användningsområden idag i den här moderna eran som den används i finansbranschen, vetenskaplig forskning och var inte. Men det är dock viktigt att veta att korrelation har tre huvudtyper av relationer. Den första är en positiv relation, som anger om det finns en förändring i värdet på en variabel, då kommer det att ske en förändring i den relaterade variabeln i samma riktning. På samma sätt, om det finns ett negativt förhållande, kommer den relaterade variabeln att beter sig i motsatt riktning. Om det inte finns någon korrelation, antyder r också ett nollvärde.Se bilderna nedan för att bättre förstå konceptet.









