Vad är Range Formula?
Områdesformel avser den formel som används för att beräkna skillnaden mellan det maximala värdet och minimivärdet för intervallet och enligt formeln subtraheras minimivärdet från det maximala värdet för att bestämma intervallet.
Område = det maximala värdet - det minsta värdet
Av den angivna datamängden, som ger statistiker och matematikern en bättre förståelse för datamängden, hur varierad den är. Det är det enklaste sättet att beräkna varians i statistik.
Förklaring
Det är ganska enkelt och lätt att använda eftersom formeln anger sitt maximala värde minus minimivärdet för det givna provet. Därför är avvikelsen mellan maximivärdet och minimivärdet intervallet, och även om det är enkelt att använda och förstå, så kräver det att det tolkas ordentligt.
Till exempel, om det finns en disposition i data, skulle intervallet påverkas av samma och skulle få resultatet kommer att leda till felaktig framställning. Ta ett praktiskt exempel för givna data 2, 4, 7, 7, 100 då skulle intervallet vara 100 - 2, vilket är 98, men som man kan se att dataområdet ligger under 10 men med tanke på och tolkning av data ligger inom 98 kommer att leda till felaktig framställning. Därför bör tolkningen av Range ske med vederbörlig hänsyn.
Exempel
Exempel 1
Överväg att följa given dataset 2,2,4,4, 4, 6,7,7,8, 8, 8, 9, 9, 9, 9, 9. Du måste beräkna intervallet för detta prov.
Lösning:
- Maxvärde = 9
- Minsta värde = 2
Område = 9 - 2
Räckvidd = 7
Exempel 2
Mr. Stark, en forskare som arbetar i tio år med ett företag som heter Dream moon. Herr Arora, hans handledare, genomför ett experiment om människors hälsa och har samlat in få provdata av manlig längd som är 162, 158, 189, 144, 151, 150, 151, 178, 155, 160. Han är förbryllad nu och vill veta hur mycket data varierar. Herr Stark, som är en erfaren statistiker, har kontaktats av sin handledare Arora för att ta bort hans förvirring om variationen i formeln. Herr Arora är skyldig att ge svar till sin handledare; du måste beräkna hur mycket data varierar?
Lösning:
Område = maximalt värde - minimivärde
- Maxvärde = 189
- Minsta värde = 144
Räckvidd = 189 - 144
Räckvidd = 45
Uppgifterna eller det samlade urvalet har en variation på 45.
Exempel # 3
Mr. Buffet, en känd och uppskattad investerare runt om i världen, överväger nu amerikanska marknadsandelar och håller på att analysera några av dem där han vill investera. Listan innehåller stora blue chip-företag i USA. Nedan visas de angivna aktierna eller värdepappren tillsammans med deras senaste börskurs, som anges i US $, där han överväger att investera i.
Du måste beräkna Range och komma med den variation listan har.
Lösning:
Nedan ges data för beräkning av intervallet.
Med hjälp av ovanstående information kommer beräkningen av Maxvärde i excel att vara som följer,

Maxvärde = 204,66
Beräkning av minvärde i excel enligt följande,
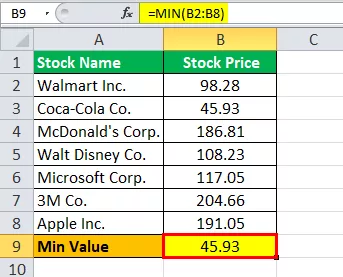
Minvärde = 45,93
Därför är beräkningen av intervallet som följer,

Område = 204,66 - 45,93
Räckvidden kommer att vara -
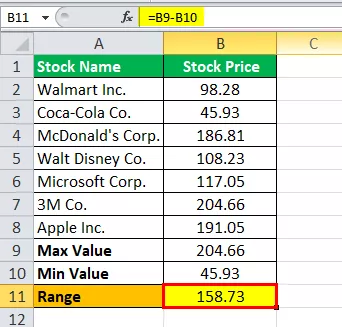
Räckvidd = 158,73
Användning av Range Formula
Området är på sitt sätt väldigt enkelt och väldigt enkelt att förstå hur siffrorna i den givna datamängden eller det givna urvalet är spridda eftersom det, som tidigare nämnts, är relativt enkelt att göra beräkningen eftersom endast krävs av en mycket grundläggande aritmetisk operation som bara subtraherar det minsta från det maximala värdet, men området det har några fler applikationer för en given datamängd eller ett visst prov i statistik. Området är också användbart för att uppskatta ett annat mått på spridning, som kallas varians eller standardavvikelsen.
Området, som nämnts tidigare, kan endast informera om de grundläggande detaljerna, dvs var spridningen av ett givet sampel eller en given uppsättning data kommer att ligga. Genom att ge skillnaden eller säga variansen mellan de högsta och de lägsta värdena för ett visst prov eller en given dataset ger det en information eller en grov uppfattning om de betydande extrema observationerna om hur utbrett de är, men återigen ger det ingen ledtråd eller någon information om de andra datapunkterna där de skulle ligga, vilket är den största svagheten i att använda intervallekvationen.
Området, som diskuterats ovan, är användbart för att skildra spridningen inom ett givet prov eller en given dataset och används vidare för att jämföra den resulterande spridningen mellan samma givna prov eller samma givna datamängder.








